Numeric Classes
In the figure the class hierarchy of the numeric classes; some methods of the classes are listed in the figure.
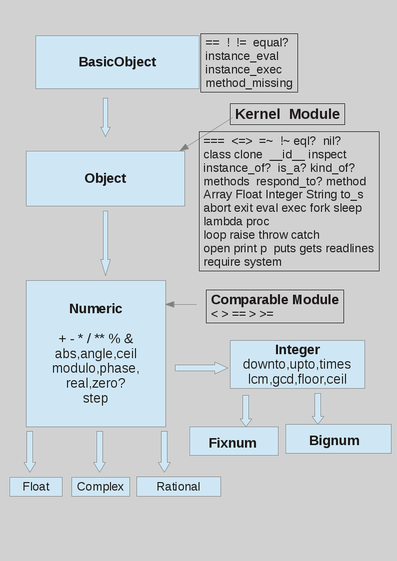
The classes for numbers are: Float, Complex, Integer, Rational; there are two subclass of Integer: Bignum and Fixnum; Bignum are numbers with an arbitrary number of digits; Fixnum are 8 bytes long integers, (but different platform can have different lengths); conversion between Bignum and Fixnum is automatically managed by Ruby: when a number is less than about 4E9 it's a Fixnum, otherwise it is a Bignum. Integer numbers can be built with the Integer method, converting its argument to an integer. Integers can also be expressed in hexadecimal, octal or binary form:
0x is the prefix for hexadecimal representations
0b is the prefix prefix for binary representation
0 is the prefix prefix for octal representation
Floats are double precision , always a digit is needed before and after the point: ".1" or "1." are not valid float numbers. "e" or "E" is before the (optional) exponent. Float numbers can be built with the Float method, converting its argument to a float number.
There are two special values for floats: "infinite" and "nan", to deal with float division by zero, but integer division by zero raises the exception: ZeroDivisionError
0.0/0.0 => NaN 1.0/0.0 => Infinity 0/0 => ZeroDivisionError: ....
Rational numbers are the ratio of two integers, used to express periodic numbers without a loss of precision. Complex numbers are printed as sum of a real and an imaginary part. Es.: (2+5i) .
Rational and complex have some specific methods and can be built with the "Rational and Complex methods:
Complex(1) => (1+0i)
Complex(2, 3) => (2+3i)
Complex(0.3) => (0.3+0i)
Complex('0.3-0.5i') => (0.3-0.5i)
Complex(2, 3).real => 2 # real part
Complex(2, 3).imag => 3 # imaginary part)
Complex(2, 3).conj => (2-3i)
Complex(0,1).phase => 1.5707963267948966 # radians
Complex(0,1).polar => [1, 1.5707963267948966] # modulus, phase
Complex(0,1).rect => [0, 1] # Array with real and imaginary parts
a=Rational("1/2")
a=1.quo(5) # division between integers that gives a rational number
Rational(1) => (1/1)
Rational(2, 3) => (2/3)
Rational(4, -6) => (-2/3)
Rational('0.3') => (3/10)
Rational('2/3') => (2/3)
Rational('0.5') => (1/2)
(Rational(3,2)).numerator => 3
(Rational(3,2)).denominator => 2
(Rational(3,2)).truncate => 1
(Rational(3,2)).round => 2
Underscores can be used inside numbers to separate digits:
a=1_000_000 => 1000000 b=2_000.0_1 => 2000.01
Methods for the Numeric Classes
All numerical operators are implemented as methods of the Numeric class: for this reason a function-like notation is legal for operators: "1.+(2)" can be used, and returns the number 3, as: "1+2".
The comparison operators: < ; > ; <= ; >=, == ; between? are implemented in the Comparable module; each numeric class implements in a different way only the operator: <=> (sometimes named: spaceship operator); the Comparable operators use the <=> operator of the specific class to give results. This mechanism is similar to the use virtual functions of the C++ language.
In the following table the most used methods of Numerics are included, also those which apply only to some subclasses of Numerics.
| Operator | Function | Examples |
|---|---|---|
| ** ; pow(x,y) | power | a**3 |
| * / | Multiplication,division | a*b ; 3*2 => 6 ; 3/2=1 |
| % | Remainder | 5/2. => 1.0 |
| + - | Addition, subtraction | a+b ; 2+5 => 7 |
| << >> | bitwise shift | 4<<1 => 8 |
| & | ^ | bitwise and, or, xor | |
| <=> | comparisons, returns: -1, 0 , 1 ; if less, equal greater | |
| < > <= >= | comparisons | 4<1=> false |
| between? | inclusion in a range | 2.between?(1,4) => true |
| == != | equal, not equal | |
| zero? | true if zero | 3.2.zero? => false |
| eql? | same value AND type | 1.0.eql? 1 => false |
| equal? | reference equality: if a is the same object as b: a.equal?(b) => true | |
| abs ; magnitude | Absolute value | -1.abs => 1 |
| abs2 | square modulus | -2.abs2 => 4 |
| ceil | minimum greater integer | 1.2.ceil => 2 ; -1.2.ceil => -1 |
| floor | maximum lower integer | 1.7.floor =>1 ; -1.2.floor =>-2 |
| round | rounds a number | 1.4.round => 1 ; 1.5.round => 2 |
| div | integer division | 5.2.div(2.0) => 2 |
| divmod | quotient and remainder | 5.divmod(2) => Array :[2, 1] |
| fdiv | float division | 3.fdiv(2) => 1.5 |
| quo | division with maximum precision (Rational numbers if integer operands) | |
Methods for Integers
| even? | true if even | 2.even? => true |
| odd? | true if odd | 3.odd? => true |
| next ; succ | next integer | 1.next => 2 |
| pred | previous integer | 2.pred =>1 |
| gcd | greatest common denominator | 10.gcd(15) => 5 |
| lcm | lowest common multiple | 10.lcm 15 => 30 |
Methods for Floats
| finite? | true if finite | (1.0/0.0).finite? => false |
| infinite? | test if infinite | (-1.0/0.0).infinite? => -1 |
| nan? | test if not a number | (0.0/0.0).nan? => true |
Conversion Methods
**to_s** # converts to string, for fixmum the argument is the base, es.:
16.to_s => "16" ;
16.to_s(2) => "10000" ;
16.to_s(16) => "10"
**to_i** # converts to integer;
**to_f** # converts to float;
**to_r** # converts to rational
Subscript Operator
The subscript operator "[]" can be used for Fixnum, and returns single bits of a number:
2[0] => 0 2[1] => 1 3[0] => 1 3[1] => 1 3[2] => 0
Precedence for operators
In the following some operators are listed, ordered by precedence (high to low precedence):
[ ] [ ]= ** ! ~ + - (unary operators) * / % + - >> << & ^ | <= < > >= <=> == === != =~ !~ && || .. ... ?: = %= /= -= += |= &= >>= <<= *= &&= ||= **= ^= not or and if unless while until begin/end